Det fortelles om en matematikklærer som fortvilet så ut over klassen og utbrøt: “Fortsetter dere slik, kommer minst 50 prosent til å stryke til eksamen.” Klassens lyse hode kommenterte straks: “Hæh? Så mange er vi ikke!” Historien er ikke stedfestet, men kan komme fra en eller annen journalistutdanning.
Min matematikkutdannelse begrenser seg til det vi lærte på gymnasets engelsklinje. Den gangen måtte man øke med 100 prosent for å fordoble. I dag kreves ikke så mye, i følge to eksempler fra NRK:
Salg av gårdssider: 25.10.2016, NRK Dagsnytt, Thor Albert Frøsland:
Kontantstøtte: 31.10. 2016, NRK Dagsnytt, Ida Creed:
I de to eksemplene ovenfor er feilregningen lett å oppdage, særlig i innslaget om kontantstøtte. Men hva med dette eksempelet, også det fra NRK?
Politihøgskolen: 28.10.2016, NRK Alltid nyheter, Jørgen Pettersen:
Mitt resonnement er slik. Antallet kvinnelige studenter i 2006 var x, antallet økte med 0,1 x (10 %) de følgende ti årene og nådde 42 i 2016. Oppstilt som ligning ser det slik ut:
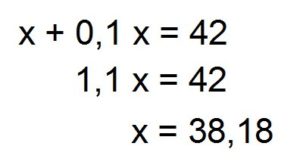
Etter min beregning ut fra NRK-reportasjen var det altså 38,18 prosent kvinnelige studenter på Politihøgskolen i 2006 hvis økningen frem til 2016 var på 10 %.
Høgskolens egen statistikk viser en kvinneandel i 2006 på 32 prosent (helt nøyaktig: 32,6 prosent). Journalistens resonnement må da ha vært at når andelen i dag er 42 prosent og for ti år siden var 32 prosent, har økningen vært på på ti prosent (42 minus 32). Hadde han brukt benevnelsen prosentpoeng om økningen, ville resonnementet vært riktig.
Så funderer jeg fortsatt på antallet krefttilfeller blant brannmenn sammenliknet med befolkningen ellers. Forholdet presenteres slik av NRK:
Kreftstatistikk: 27.10.2016, NRK Dagsnytt, Marit Gjellan:
Jeg har prøvd meg på følgende resonnement:
– De som får kreft blant brannmenn er 25% av de undersøkte.
– Tilsvarende gruppe (alle som får kreft) ellers i befolkningen er 80 % av prosentandelen som får kreft blant brannmenn (100 % – 80 %) .
– 80 % av en prosentandel på 25 blir en prosentandel på 20 , dvs. at 20 % av befolkningen får kreft.
– Når befolkningen er på ca. 5 millioner, utgjør 20 prosent 1 million.
Men for min bekjentskapskrets stemmer det ikke at hver femte person har kreft. Derfor har jeg en mistanke om at det også i dette nyhetsinnslaget er en sammenblanding av prosent og prosentpoeng. Men jeg har ikke funnet statistisk belegg for dette, og mottar gjerne hjelp.
___________________________________________________________________________
Vil du følge denne bloggen? Registrer deg øverst i spalten til venstre, så mottar du hver lørdag melding om innholdet i ukens blogg. |